|
Let H(κ) = T + κB∗A be a
self-adjoint perturbation of the self-adjoint operator T, and suppose that T has an
eigenvalue λ0 of finite multiplicity m embedded in its continuous spectrum. If the
operator
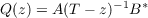
is bounded and can be continued meromorphically across the axis at λ0, the
asymptotic spectral concentration of the family H(κ) at λ0 is determined by the
poles of
![κA(H (κ)− z)−1B∗ = I − [I + κQ(z)]−1](a131x.png) | (1) |
These “resonances” can be expanded in a series of fractional powers of κ, and
therefore have a unitarily invariant significance for the family H(κ). An example
shows that nonanalytic series may indeed occur; however, if a resonance is an actual
eigenvalue of H(κ) for all sufficiently small real κ, its series is analytic. Because the
resonances cannot lie on the first sheet when κ is real, these series must have a
special form. In the generic case, they yield, as the lowest order approximation to the
imaginary parts of the resonances, the famous Fermi’s Golden Rule. The case when
λ0 is embedded at a branch point of (1) is studied by means of a simple
example.
|





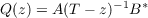
![κA(H (κ)− z)−1B∗ = I − [I + κQ(z)]−1](a131x.png)
