|
|||||

|

|
|

|

|
|
Stieltjes
differential-boundary operators. II
Allan Morton Krall |
|
Vol. 55 (1974), No. 1, 207–218
|
Abstract |
|
The differential boundary system ![Ly = (y+ H [Cy (0)+ Dy(1)]+ H1Ψ)′ + P y,](a160x.png)
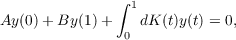
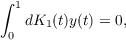 and its adjoint system are written as Stielties integral equation systems with end point boundary conditions. Fundamental matrices are exhibited and, from these, a spectral analysis and a Green’s matrix are produced. These are used to achieve spectral resolutions in both self-adjoint and nonself-adjoint situations. |
Mathematical Subject Classification 2000
Primary: 34B25
Secondary: 47E05
|
Milestones
Received: 7 March 1974
Published: 1 November 1974
|
Authors |
| Allan Morton Krall | |
 |
