A product integral solution of a Riccati equation

Burrell Washington Helton

Vol. 56 (1975), No. 1, 113–130

DOI: 10.2140/pjm.1975.56.113

Abstract

Product integrals are used to show that, if dw, G, H and K are functions from number pairs to a normed complete ring N which are integrable and have bounded variation on [a,b] and v⁻¹ exists and is bounded on [a,b], then the integral equation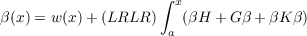

has a solution β(x) = v⁻¹(x)u(x) on [a,b], where u and v are defined by the matrix equation

The above results are used to show that if p,q,h and r are quasicontinuous functions from the numbers to N such that h is left continuous and has bounded variation and p,q and h commute, then the solution on [a,b] of the differential-type equation f^∗∗ + f^∗p + fq = r is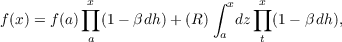

where f(x) − f(a) = (L)∫ _a^xf^∗dh, β is the solution of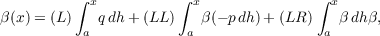

and z is defined in terms of p,q,r,h and β.

Mathematical Subject Classification 2000

Primary: 34A99

Secondary: 26A39, 45A05

Milestones

Received: 12 September 1973

Revised: 11 June 1974

Published: 1 January 1975