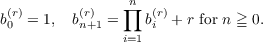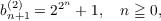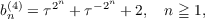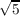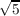|
For every real r ≧ 0, there is a
sequence {bn(r)} defined by
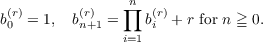 | (1) |
These sequences were considered previously, in [1], for integer values of r, and it was
shown that there is a constant 𝜃 = 𝜃(r) such that
 | (2) |
for each r = 1,2,3,⋯ . It was observed that
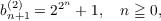 | (3) |
whereby 𝜃(2) = 2, and the problem was proposed “to determine the algebraic or
transcendental character of the real numbers 𝜃(r) for r = 1,3,4,5,6,⋯.”
In this paper, we observe explicitly (in §II) that
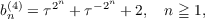 | (4) |
where τ = (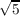 + 1)∕2 = 1.618⋯ is the “Golden Mean”, and thus
𝜃(4) = τ2 = ( + 1)∕2 = 1.618⋯ is the “Golden Mean”, and thus
𝜃(4) = τ2 = (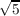 + 3)∕2 = 2.618⋯ . + 3)∕2 = 2.618⋯ .
|