|
I. Introduction. Consider the
Dirichlet problem for a bounded domain G ⊂ Rn(n ≧ 2) having smooth boundary
∂G:
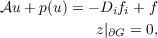 | (1) |
where 𝒜 is a second order differential operator of Leray-Lions type mapping a real
Sobolev space W01q(G)(1 < q < ∞) into its dual; f,fi(i = 1,⋯,n) are given
functions. We have used the notation Di for the derivative in the distribution sense
∂∕∂xi and the convention that if an index is repeated then summation over that
index from 1 to n is implied. We shall assume that the real function p(t) is
continuous and satisfies the condition
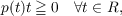 | (2) |
but otherwise (p)t is not subject to any growth condition.
In this paper we discuss the existence of a solution of equation (1) in
W01,q(G) ∩ L∞(G).
|