Multiplicative operations in BP^∗BP

Douglas Conner Ravenel

Vol. 57 (1975), No. 2, 539–543

DOI: 10.2140/pjm.1975.57.539

Abstract

One of the present computational difficulties in complex cobordism theory is the lack of a known algebra splitting of BP^∗BP, the algebra of stable cohomology operations for the Brown-Peterson cohomology theory, analogous to the splitting isomorphism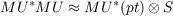

where S is the Landweber-Novikov algebra. S has the added advantage of being a cocommutative Hopf algebra over Z. This paper does not remove this difficulty, but we will show that the monoid of multiplicative operations in BP^∗BP, (i.e. those operations which induce ring endomorphisms on BP^∗X for any space X), which we will denote by Γ(BP), has a submonoid analogous to the monoid of multiplicative operations in S.

Mathematical Subject Classification 2000

Primary: 55G25

Secondary: 14L05

Milestones

Received: 4 December 1974

Published: 1 April 1975