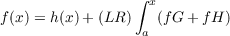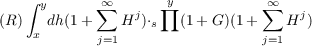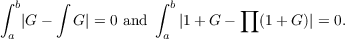|
Functions are from R to N
or R × R to N, where R denotes the set of real numbers and N denotes
a normed complete ring. If β > 0,H and G are functions from R × R to
N,f and h are functions from R to N, each of H,G and dh has bounded
variation on [a,b] and |H| < 1 − β on [a,b], then the following statements are
equivalent:
(1) f is bounded on [a,b], each of ∫
abH,∫
abG and (LR)∫
ab(fG + fH) exists
and
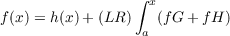
for a ≦ x ≦ b, and
(2) each of ⋅x ∏
y(1 + ∑
j=1∞Hj), ⋅x ∏
y(1 + G) and
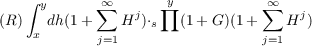
exists for a ≦ x < y ≦ b and
| f(x) | = h(a)⋅a ∏
x(1 + G)(1 + ∑
j=1∞Hj) | |
| | + (R)∫
axdh(1 + ∑
=1∞Hj)⋅
s ∏
x(1 + G)(1 + ∑
j=1∞Hi) | | |
for a ≦ x ≦ b. This result is obtained without requiring the existence of integrals of
the form
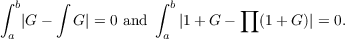
|