|
|||||

|

|
|

|

|
|
Covering the vertices
of a graph by vertex-disjoint paths
Shahbaz Noorvash |
|
Vol. 58 (1975), No. 1, 159–168
|
Abstract |
|
Define the path-covering number μ(G) of a finite graph G to be the minimum number of vertex-disjoint paths required to cover the vertices of G. Let g(n,k) be the minimum integer so that every graph, G, with n vertices and at least g(n,k) edges has μ(G) ≦ k. A relationship between μ(G) and the degree sequence for a graph G is found; this is used to show that 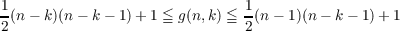 A further extremal problem is solved. |
Mathematical Subject Classification 2000
Primary: 05C35
|
Milestones
Received: 30 November 1973
Published: 1 May 1975
|
Authors |
| Shahbaz Noorvash | |
 |
