A new characterization of characteristic functions of absolutely continuous distributions

Simeon M. Berman

Vol. 58 (1975), No. 2, 323–329

DOI: 10.2140/pjm.1975.58.323

Abstract

It is well known that if g belongs to L₂, then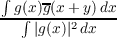

is the characteristic function of an absolutely continuous distribution function. Conversely, every such characteristic function has the representation given above. Rere we shown that if R(s,t) is a covariance function such that R(s,s) belongs to L₁, then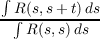

is the characteristic function of an absolutely continuous distribution. Conversely, every such characteristic function has the latter representation (put R(s,t) = g(s)g(t)). The use of this new result is that certain functions are directly seen to be of the second form but not the first; hence, they can be identifled as characteristic functions of absolutely continuous distributions.

Mathematical Subject Classification 2000

Primary: 60G10

Secondary: 60E05

Milestones

Received: 18 March 1974

Published: 1 June 1975