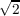On Gross differentiation on Banach spaces

Hui-Hsiung Kuo

Vol. 59 (1975), No. 1, 135–145

DOI: 10.2140/pjm.1975.59.135

Abstract

Let p_t(x,⋅) denote the Wiener measure in an abstract Wiener space (H,B) with variance parameter t > 0 and mean x in B. It is shown that if f ∈ L²p_t(x,⋅),t > 0 and x are fixed, then the function p_tf defined by p_tf(x + h) = ∫ _Bf(y)p_t(x + h,dy) for h in H is infinitely Gross differentiable at x. The first two derivatives are given by (Dp_tf(x),h) = t⁻¹ ∫ _Bf(y)(h,y −x)p_t(x,dy) and (D²p_tf(x)k,h) = t⁻¹ ∫ _Bf(y){t⁻¹(h,y −x)(k,y −x) − (h,k)}p_t(x,dy), where h and k are in H. Moreover, D²p_tf(x) is a Hilbert-Schmidt operator and ∥D²p_tf(x)∥₂ ≦ t⁻¹{∫ _B|f(y)|²p_t(x,dy)}1∕2. An application to Uhlenbeck-Ornstein process is also given.

Mathematical Subject Classification 2000

Primary: 28A40

Secondary: 60J65, 58D15

Milestones

Received: 7 March 1975

Published: 1 July 1975