|
|||||

|

|
|

|

|
|
On the inequality
∑ i=1npi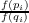 ≧ 1 ≧ 1
Pál Fischer |
|
Vol. 60 (1975), No. 1, 65–74
|
Abstract |
|
We show that the inequality 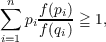 for all P,Q ∈ An = |
Mathematical Subject Classification 2000
Primary: 94A15
|
Milestones
Received: 10 June 1974
Published: 1 September 1975
|
Authors |
| Pál Fischer | |
 |
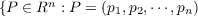 where
where 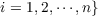 and some integer
and some integer 