The Diophantine equation Y (Y + m)(Y + 2m)(Y + 3m) = 2X(X + m)(X + 2m)(X + 3m)

S. Jeyaratnam

Vol. 60 (1975), No. 1, 183–187

DOI: 10.2140/pjm.1975.60.183

Abstract

J. H. E. Cohn has shown that the equation of the tltle has only four pairs of nontrivial solutions in integers when m = 1. The object of this paper is to prove the following two theorems concerning the solutions of the equation of the title:

Theorem 1. The equation of the title has only four pairs of nontrivial solutions in integers given by X = 4m or −7m, Y = 5m or −8m when m is of the form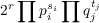

where r, s_i’s and t_j’s are nonnegative integers, p_i’s are positive primes ≡ 3,5 (mod 8) and q_i’s are positive primes ≡ 1 (mod 8) such that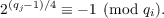

Theorem 2. The only positive integral solution of the equation of the title, for all positive integral values of m ≦ 30, is X = 4m, Y = 5m.

Mathematical Subject Classification

Primary: 10B10

Milestones

Received: 27 March 1974

Revised: 22 November 1974

Published: 1 September 1975