Unconditional Schauder decompositions of normed ideals of operators between some l_p-spaces

Y. Gordon

Vol. 60 (1975), No. 2, 71–82

DOI: 10.2140/pjm.1975.60.71

Abstract

Given a Banach space E, let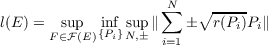

where ℱ(E) denotes the collection of all finite-dimensional subspaces of E, the infimum ranges over all possible sequences of finite-rank operators P_i : F → E which satisfy the equality ∑ P_i(f) = f for all f ∈ F, and r(P) denotes the rank of an operator P.

It is shown that there are finite-dimensional spaces with arbitrarily large l(E) values, and infinite-dimensional spaces E with l(E) = ∞. The specific examples with l(E) = ∞ yield also information on the rapidity of growth of unconditional Schauder decompositions of E into finite-dimensional spaces.

Mathematical Subject Classification 2000

Primary: 47D15

Secondary: 46B15

Milestones

Received: 29 April 1975

Published: 1 October 1975