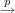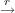On a space between BH and B_∞

Jerrold Norman Siegel

Vol. 60 (1975), No. 2, 235–246

DOI: 10.2140/pjm.1975.60.235_

Abstract

Let F ⊆ E_∞B _∞ be the classifying space of fibre homotopy equivalence classes of fibrations with fiber F. An obstruction to the existence of a retraction B_∞E_∞ is developed. This obstruction is shown to vanish when F is a stable space. Consequences of the existence of a retraction are indicated.

Mathematical Subject Classification

Primary: 55F15

Milestones

Received: 7 January 1974

Revised: 25 April 1974

Published: 1 October 1975