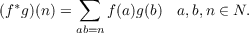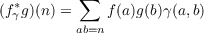Generalized convolution ring of arithmetic functions

Ingrid Fotino

Vol. 61 (1975), No. 1, 103–116

DOI: 10.2140/pjm.1975.61.103

Abstract

1. Introduction. The set of arithmetic functions has the structure of a unitary associative ring under functional addition and the convolution operation defined by

(1.1)

It is also a unique factorization domain with respect to convolution.

The purpose of this paper is to determine the conditions under which this structure is preserved when the concept of convolution is generalized to include a weighting kernel γ:

(1.2)

Mathematical Subject Classification 2000

Primary: 10A20, 10A20

Secondary: 20M05

Milestones

Received: 23 July 1974

Revised: 3 September 1975

Published: 1 November 1975