A ratio limit theorem for a strongly subadditive set function in a locally compact amenable group

John Cronan Kieffer

Vol. 61 (1975), No. 1, 183–190

DOI: 10.2140/pjm.1975.61.183

Abstract

It is the purpose of this paper to prove that the following property holds: Given a locally compact, amenable, unimodular group G, if S is a strongly subadditive, nonpositive, right invariant set function defined on the class 𝒦 of relatively compact Borel subsets of G, and if {A_α} is a net in 𝒦 satisfying an appropriate growth condition, then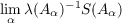

exists independently of {A_α}, where λ is Haar measure on G.

Mathematical Subject Classification 2000

Primary: 43A05

Secondary: 60B15, 28A65

Milestones

Received: 15 May 1975

Published: 1 November 1975