|
|||||

|

|
|

|

|
|
Properties which normal
operators share with normal derivations and related
operators
Joel Hilary Anderson and Ciprian Foias |
|
Vol. 61 (1975), No. 2, 313–325
|
Abstract |
|
Let S and T be (bounded) scalar operators on a Banach space 𝒳 and let C(T,S) be the map on ℬ(𝒳), the bounded linear operators on 𝒳, defined by 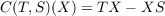 for X in ℬ(𝒳). This paper was motivated by the question: to what extent does C(T,S) behave like a normal operator on Hilbert space? It will be shown that C(T,S) does share many of the special properties enioyed by normal operators. For example it will be shown that the range of C(T,S) meets its null space at a positive angle and that C(T,S) is Hermitian if T and S are Hermitian. However, if ℋ is a Hilbert space then C(T,S) is a spectral operator if and only if the spectrum of T and the spectrum of S are both finite. |
Mathematical Subject Classification 2000
Primary: 47B47
|
Milestones
Received: 25 October 1974
Published: 1 December 1975
|
Authors |
| Joel Hilary Anderson | |
| Ciprian Foias | |
| http://www.indiana.edu/~alldrp/members/foias.html | |
 |
