An inversion of the S₂ transform for generalized functions

L. S. Dube

Vol. 61 (1975), No. 2, 383–390

DOI: 10.2140/pjm.1975.61.383

Abstract

Define S₂ transform of a member f of a certain space of generalized functions as

where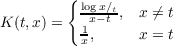

(0 < t < ∞,0 < x < ∞).

It is shown that

in the weak distributional sence. Here H_n,x is a certain linear generalized differential operator.

Mathematical Subject Classification 2000

Primary: 46F10

Secondary: 44A05

Milestones

Received: 10 December 1974

Revised: 24 July 1975

Published: 1 December 1975