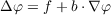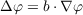|
Consider the equations in
Rn, n ≧ 2,
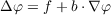 | (*) |
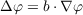 | (I) |
where f and b are locally Hölder continuous, and as |x|→∞, f(x) = O(|x|−τ),
b(x) = O(|x|−σ), σ,τ > 1. It is shown that if 0 ≦ ρ < σ − 1, there is a one-to-one
correspondence between entire C2 solutions of (∗) whose gradients grow
no faster than O(|x|ρ), and harmonic polynomials with gradients of the
same growth. For (I) therefore solutions whose gradients grow no faster than
O(|x|ρ) form a finite dimensional vector space. These results for (I) give
analogues to the concept of “generating pairs” in pseudo-analytic function
theory.
|