Uniform algebras spanned by Hartogs series

Theodore William Gamelin

Vol. 62 (1976), No. 2, 401–417

DOI: 10.2140/pjm.1976.62.401

Abstract

Let A be a uniform algebra on a compact space X, and let R be an upper semi-continuous function from X to [0,∞). Let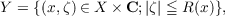

and let B be the uniform algebra on Y generated by polynomials in ζ with coefficients in A. The maximal ideal space M_B of B then has the form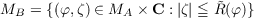

for some function R on M_A. We will give several characterizations of R in terms of R. One description involves Hartogs functions, another involves Jensen measures. We will also treat the problem of characterizing the continuous functions on M_B which lie in the algebra B.

Mathematical Subject Classification 2000

Primary: 46J10

Milestones

Received: 21 May 1975

Published: 1 February 1976