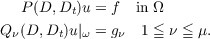|
Let P(D,Dt) be a hypoelliptic
differential operator with constant coefficients of type μ with index of hypoellipticity
equal to d ≧ 1. Let Ω be an open subset of the half space R+n+1 with plane piece of
boundary ω contained in R0n. Let Q1(D,Dt),⋯,Qμ(D,Dt) be μ partial
differential operators with constant coefficients and consider the boundary value
problem:
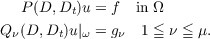 | (1) |
In this paper necessary and sufficient conditions are given on Q1,⋯,Qμ in order
that all solutions u of (1) shall belong to the Gevrey class of index d in Ω ∪ ω
whenever the initial data belong to such classes of functions. In particular, we give
not only algebraic conditions but also show how to construct a parametrix for such
problems.
|