|
0. Introduction. In
this paper we introduce the concept of “Cycles in the Period” of the simple
continued fraction expansion of a real quadratic irrational. This is expressed in
the
Definition. Let M, D, d be positive rational integers, M square free,
M = D2 + d, d ≦ 2D. Let k, a, s be nonnegative rational integers, 0 ≦ a ≦ k − 1; let
f = f(k,a,s;d,D) be a polynomial with rational integral coefficients. For a fixed s,
the finite sequence of polynomials
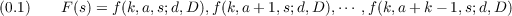
will be called “Cycle in the Period” of the simple continued fraction expansion of
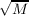 if, for s0 ≧ 1, this expansion has the form if, for s0 ≧ 1, this expansion has the form
![√ --- ------------------------------------------
(0.1) M = [b0,b1,⋅⋅⋅ ,F(0),⋅⋅⋅ ,F (s0 − 1),f(k,a,s0;d,D ),⋅⋅⋅,
f(k,a+-b,s0;d,D-),⋅⋅⋅ ,f(k,a,s0;d,D-),F-′(s0 −-1),⋅⋅⋅ ,
------------------------------
F ′(0),f(k,a − 1,0;d,D ),⋅⋅⋅ ,b1,2b0 ]](a032x.png)
b ≧ 1;b ≦ k − 1;k is the length of the cycle; F′(s) means that the order of the f −s
must be reversed.
In the first part of this paper, the main result is the construction of infinitely
many classes of quadratic fields Q(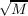 ), each containing infinitely many M of a
simple structure. Among the various classes thus constructed, there are a few in
whose expansion of ), each containing infinitely many M of a
simple structure. Among the various classes thus constructed, there are a few in
whose expansion of 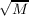 cycles in the period surprisingly have the length ≦ 12.
Functions f(k,a,s;d,D), f(k,a + 1,s;d,D),⋯ are of course stated explicitly; hence
we are able to construct numbers cycles in the period surprisingly have the length ≦ 12.
Functions f(k,a,s;d,D), f(k,a + 1,s;d,D),⋯ are of course stated explicitly; hence
we are able to construct numbers 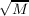 such that the primitive period of
their expansion has any given length m which is a function of the parameter
k. such that the primitive period of
their expansion has any given length m which is a function of the parameter
k.
|




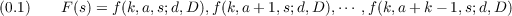
![√ --- ------------------------------------------
(0.1) M = [b0,b1,⋅⋅⋅ ,F(0),⋅⋅⋅ ,F (s0 − 1),f(k,a,s0;d,D ),⋅⋅⋅,
f(k,a+-b,s0;d,D-),⋅⋅⋅ ,f(k,a,s0;d,D-),F-′(s0 −-1),⋅⋅⋅ ,
------------------------------
F ′(0),f(k,a − 1,0;d,D ),⋅⋅⋅ ,b1,2b0 ]](a032x.png)

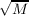 if, for
if, for 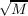
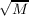 cycles in the period surprisingly have the length
cycles in the period surprisingly have the length 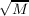 such that the primitive period of
their expansion has any given length
such that the primitive period of
their expansion has any given length 