|
|||||

|

|
|

|

|
|
Interpolating sequences
for functions satisfying a Lipschitz condition
Eric P. Kronstadt |
|
Vol. 63 (1976), No. 1, 169–177
|
Abstract |
|
Let D be the unit disk in C, Lip (D) the space of functions, f, holomorphic in D, continuous on D and satisfying a Lipschitz condition: 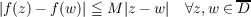 If S = {ai}x=1∞∈ D is a discrete sequence with no accumulation points in D, let Lip (S) be the set of functions, g, defined on S satisfying 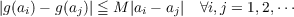 We say S is a Lip (D) interpolating (LI) sequence if the restriction mapping from Lip (D) to Lip (S) given by f → f|S is surjective. Our aim is to describe some of the properties of such sequences and to give some examples. Specifically we show that an LI sequence must either be a uniformly separated sequence, or the union of two such sequences which approach one another as they tend to ∂D. |
Mathematical Subject Classification
Primary: 30A80, 30A80
|
Milestones
Received: 4 November 1974
Published: 1 March 1976
|
Authors |
| Eric P. Kronstadt | |
 |
