Functional relationships between a subnormal operator and its minimal normal extension

Robert Olin

Vol. 63 (1976), No. 1, 221–229

DOI: 10.2140/pjm.1976.63.221

Abstract

Let K be a compact subset of the plane. C(K) denotes the continuous functions on K and R(K) denotes those continuous functions of K which are uniform limits of rational functions whose poles lie off K. We say that f is minimal on K if f ∈ R(K) and for every complex number c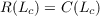

where L_c = {z ∈ K|(fz) = c}.

Let S be a subnormal operator on a Hilbert space ℋ with its minimal normal extension N on the Hilbert space 𝒦. The spectrum of S is denoted by σ(S). In this paper it is shown that if f is minimal on σ(S) then f(N) on 𝒦 is the minimal normal extension of f(N) restricted to ℋ. Some new results about subnormal operators follow as corollaries of this theorem.

Mathematical Subject Classification 2000

Primary: 47B20

Milestones

Received: 28 July 1975

Published: 1 March 1976