Bounds and quantitative comparison theorems for nonoscillatory second order differential equations

Thomas Thornton Read

Vol. 63 (1976), No. 1, 231–245

DOI: 10.2140/pjm.1976.63.231

Abstract

A lower bound is given for the positive increasing solution of y′′ + 2ry′−q²y = 0 on the interval [0,∞) and an upper bound is given for the positive decreasing solution of this equation. These are used to estimate z∕y and z₀∕y₀ where y and z (respectively y₀ and z₀) are positive nonprincipal (respectively principal) solutions of nonoscillatory equations y′′−p₁y = 0 and z′′−p₂z = 0 for which p₂ ≧ p₁. A special case of one result is that if p₁ is bounded and if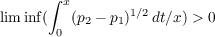

as x →∞ then z∕y increases exponentially and z₀∕y₀ decreases exponentially.

Mathematical Subject Classification 2000

Primary: 34C10

Milestones

Received: 18 June 1975

Revised: 19 December 1975

Published: 1 March 1976