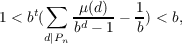|
In 1971, J. M. Gandhi showed
that if the first n primes, p1,p2,⋯,pn are known, then the next prime, pn+1, is given
“explicitly” by the formula:
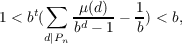 | (1) |
where b is any positive integer ≧ 2, where Pn = p1p2⋯pn, where μ(d) is the Möbius
function, and where the unique integer value of t which satisfies the indicated
inequalities is in fact pn+1.
In this paper, we obtain of the following formulas for pn+1:
| pn+1 | = lims→∞{Pn(s)ζ(s) − 1}−1∕s | (2)
| | pn+1 | = lims→∞{Pn(s) − ζ−1(s)}−1∕s | (3)
| | pn+1 | = lims→∞{ζ(s) − Qn(s)}−1∕s | (4)
| | and | |
| | pn+1 | = lims→∞{1 − ζ−1(s)Q
n(s)}−1∕s. | (5) |
|