|
|||||

|

|
|

|

|
|
The splitting of
extensions of SL(3,3) by the vector space F33.
Robert L. Griess, Jr. |
|
Vol. 63 (1976), No. 2, 405–409
|
Abstract |
|
We give two proofs
that H2(SL(3,3),F33) = 0. This result has appeared in a paper by Sah, [6],
but our methods are relatively elementary, i.e., we require only elementary
homological algebra and do a group-theoretic analysis of an extension of
SL (3, 3) by F33 to show that the extension splits. The starting point is
to notice that the vector space is a free module for F3(⟨x⟩), where x has
Jordan canonical form |
Mathematical Subject Classification 2000
Primary: 18H10, 18H10
Secondary: 20D05
|
Milestones
Received: 31 October 1974
Published: 1 April 1976
|
Authors |
| Robert L. Griess, Jr. | |
| Department of Mathematics University of Michigan 530 Church Street Ann Arbor MI 48109-1043 United States |
|
 |
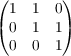 . We then can exploit the vanishing of
. We then can exploit the vanishing of
