|
|||||

|

|
|

|

|
|
Roots of the Euler
polynomials
Frederic Timothy Howard |
|
Vol. 64 (1976), No. 1, 181–191
|
Abstract |
|
In this paper we prove some
new theorems about the real and complex roots of the Euler polynomials. For each n
we show how the real roots of En(x) are distributed in the closed intervaI [1, 3].
We also show how the real roots of En(x) are distributed in the arbitrary
interval [m,m + 1] for n sufficiently large. Finally, we prove that if a and b
are nonzero rational numbers and c is a square-free integer, then En(x)
has no roots of the form a |
Mathematical Subject Classification
Primary: 30A08, 30A08
Secondary: 33A70
|
Milestones
Received: 2 December 1975
Revised: 30 March 1976
Published: 1 May 1976
|
Authors |
| Frederic Timothy Howard | |
 |
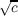
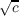 ,
, 