The solution of a Stieltjes-Volterra integral equation for rings

Burrell Washington Helton

Vol. 64 (1976), No. 2, 419–436

DOI: 10.2140/pjm.1976.64.419

Abstract

For a triple (h,K,g) of functions and an interval [a,x], the author defines a subdivision-refinement-type limit V (a,x;h,K,dg) of the set {V (D,h,K,Δg)} of determinants, where each subdivision D = {x_i}₀ⁿ of [a,x] defines an n×n determinant of the set and each determinant has the form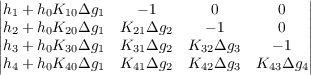

The following theorem is proved. If f, g, h and K are functions to a ring and g has bounded variation on [a,b], then (f,K,g) ∈ OA^∗ and f(x) = h(x) + (L)∫ _a^xf(t)K(x,t)dg(t) on [a,b] iff (h,K,g) ∈ OM^∗ and f(x) = V (a,x;h,K,dg) on [a,b]. The OA^∗ and OM^∗ sets are defined and sufficient conditions are proved for (f,K,g) ∈ OA^∗ and (h,K,g) ∈ OM^∗, and for the existence of the limit V (a,x;h,K,dg), and for V (a,x;h,K,dg) = h(x) − (L)∫ _a^xh(t)dV (t,x;1,K,dg).

Mathematical Subject Classification 2000

Primary: 45D05

Milestones

Received: 15 October 1974

Revised: 11 February 1976

Published: 1 June 1976