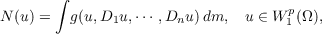|
Let Ω be a domain in Rn
and let a nonlinear functional N be given on the first order Sobolev space
W1p(Ω), 1 ≦ p ≦∞. We are concerned with obtaining a characterization of those
functionals N of the form
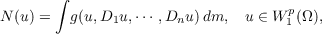 | (1.1) |
where g : Rn+1 → R is a continuous function, Diu(i = 1,⋯,n) denotes the
distribution derivative of u relative to its i-th coordinate variable and m
denotes Lebesgue measure. In the present paper we confine ourselves to the
case n = 1. The general case will be considered in the second part of this
work.
|