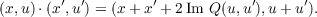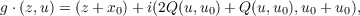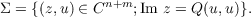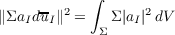Group representations on Hilbert spaces defined in terms of ∂_b-cohomology on the Silov boundary of a Siegel domain

Hugo Rossi and Michele Vergne

Vol. 65 (1976), No. 1, 193–207

DOI: 10.2140/pjm.1976.65.193

Abstract

Let Q be a Cⁿ-valued quadratic form on C^m. Let N(Q) be the 2-step nilpotent group defined on Rⁿ ×C^m by the group law

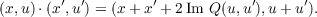
Then N(Q) has a faithful representation as a group of complex affine transformations of C^n+m as follows:

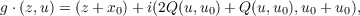
where g = (x₀,u₀). The orbit of the origin is the surface

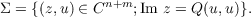
This surface is of the type introduced in [11], and has an induced ∂_b-complex (as described in that paper) which is, roughly speaking, the residual part (along Σ) of the ∂-complex on C^n+m. Since the action of N(Q) is complex analytic, it lifts to an action on the spaces E^q of this complex which commutes with ∂_b. Since the action of N(Q) is by translations, the ordinary Euclidean inner product on C^n+m is N(Q)-invariant, and thus N(Q) acts unitarily in the L²-metrics on C₀^∞(E^q) defined by

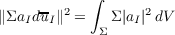
where dV is ordinary Lebesgue surface measure. In this way we obtain unitary representations ρ_q of N(Q) on the square-integrable cohomology spaces H^q(E) of the induced ∂_b-complex.

Mathematical Subject Classification 2000

Primary: 22E45

Secondary: 32M15

Milestones

Received: 8 January 1976

Published: 1 July 1976