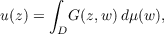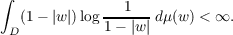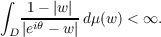Variation of Green’s potential

Jang-Mei Gloria Wu

Vol. 66 (1976), No. 1, 295–303

DOI: 10.2140/pjm.1976.66.295

Abstract

Let u be the Green’s potential of a nonnegative mass distribution μ on unit disk D, defined by

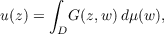(1.1)

where G is the Green’s function on D. The following will be proved.

Theorem 1. Suppose 0 < ρ < 1 and

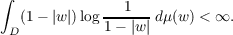(1.2)

Then for almost all 𝜃, 0 ≦ 𝜃 < 2π, u has finite variation on the line segment joining ρe^i𝜃 and e^i𝜃.

Theorem 2. Fix 𝜃, 0 ≦ 𝜃 < 2π and suppose

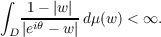(1.3)

If L is a circular arc in D centered at e^i𝜃, then for all a on L except a set of capacity zero, u has finite variation on the line segment joining a and e^i𝜃.

Mathematical Subject Classification 2000

Primary: 31A15

Milestones

Received: 10 November 1975

Revised: 1 June 1976

Published: 1 September 1976