|
Let E, X be two complex
Banach spaces, (E;X) the space of all linear bounded operators from E into X
endowed with its usual norm. We denote by 𝒟′(E) the space of distributions with
values in E defined in −∞ < t < ∞ and by 𝒟0′(E) the subspace of 𝒟′(E) consisting
of all T ∈𝒟′(E) with support in t ≧ 0.
Given P ∈𝒟0′((X;E)) we examine the following problems.
(I). Does P have a convolution inverse with support in t ≧ 0, that is, is there
S ∈𝒟0′((E;X)) satisfying
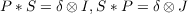 | (1.1) |
where I (resp. J) denotes the identity operator in E (resp. X) and δ is the Dirac
delta?
(II). In case the answer to (I) is affirmative, what properties of S can be deduced
from properties of P and vice versa?
|