Rational approximation to xⁿ

Donald J. Newman and A. R. Reddy

Vol. 67 (1976), No. 1, 247–250

DOI: 10.2140/pjm.1976.67.247

Abstract

This note is concerned with the approximations of xⁿ on [0,1] by polynomials and rational functions having only non-negative coefficients and of degree at most k (1 ≦ k ≦ n − 1). It is shown that the best approximating polynomial of degree k on [0,1] to xⁿ is of the form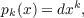

where d > 0 and satisfies the assumption that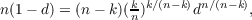

with an error 𝜖_k = 1 − d, for each fixed k = 1,2,3,⋯,n − 1. It is also shown that dx^k is a best approximating rational function of degree k to xⁿ on [0,1].

Mathematical Subject Classification 2000

Primary: 41A20

Milestones

Received: 26 May 1976

Revised: 21 July 1976

Published: 1 November 1976