Inclusion relations between power methods of limitation

Abraham Ziv

Vol. 67 (1976), No. 1, 251–275

DOI: 10.2140/pjm.1976.67.251

Abstract

Let p(x) = ∑ p_kx^k be a power series with p_k (k = 0,1,⋯) complex numbers and 0 < ρ_p ≦∞ its radius of convergence, and assume that P(x)≠0 for 0 ≦ α_p ≦ x < ρ_p. The power method of limitation, P, is defined by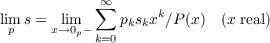

(provided the series converges in [α_p,ρ_p) and the limit exists and is finite). Abel and Borel methods are the best known power methods. In this article inclusion relations between two power methods are investigated. Several theorems are proved, which lead to necessary and sufficient conditions, for inclusion, that are correct under some fairly moderate restrictions.

Mathematical Subject Classification 2000

Primary: 40D25

Milestones

Received: 5 December 1974

Revised: 9 November 1975

Published: 1 November 1976