Integrals of continuous functions

Mark Finkelstein and Robert James Whitley

Vol. 67 (1976), No. 2, 365–372

DOI: 10.2140/pjm.1976.67.365

Abstract

Semicontinuous and related functions are characterized as integrals of continuous functions in several variables. For example: a new result of classical type is that the nonnegative lower semicontinuous functions on the real line are exactly those functions f which can be written as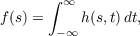

with h nonnegative and continuous on R × R and h(s,⋅) integrable. There is a similar representation for functions of Baire class 0 or 1 but the integral involved is the (conditional) improper Riemann integral. Generalization leads to a concept of conditional integrals in a more general setting.

Mathematical Subject Classification 2000

Primary: 28A25

Secondary: 26A42

Milestones

Received: 4 June 1976

Published: 1 December 1976