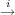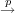|
In this paper, the following is
proved.
Theorem. Let F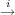 E E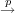 B be a fibration in which E and B have the homotopy
type of CW complexes. Suppose that F is (n − 1) connected and B is (m − 1)
connected, where m,n ≧ 2. Let l = min(m,n), k = min(2m − 1,2n). Suppose that
there exists a map E ×F → E of type (1,i). If πq(B) = 0 for all q ≧ n + l, then the
fibration is Ganea principal. If further πq(F) = 0 for all q ≧ n + k, then the
fibration is induced by some map f : B → Y for some space Y. The dual is also
true. B be a fibration in which E and B have the homotopy
type of CW complexes. Suppose that F is (n − 1) connected and B is (m − 1)
connected, where m,n ≧ 2. Let l = min(m,n), k = min(2m − 1,2n). Suppose that
there exists a map E ×F → E of type (1,i). If πq(B) = 0 for all q ≧ n + l, then the
fibration is Ganea principal. If further πq(F) = 0 for all q ≧ n + k, then the
fibration is induced by some map f : B → Y for some space Y. The dual is also
true.
|