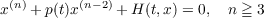Nth order oscillations with middle terms of order N − 2

Athanassios G. Kartsatos

Vol. 67 (1976), No. 2, 477–488

DOI: 10.2140/pjm.1976.67.477

Abstract

Equations of the form

(*)

are studied here, where p(t) ≧ 0 and uH(t,u) ≧ 0.

It is shown, among other things, that for n even all solutions of (∗) oscillate if H is superlinear, satisfying the usual integral conditions, and u′′ + p(t)u = 0 is nonoscillatory with p(t) “small” and decreasing. The case of n odd is also covered and some of the recent results of Waltman, Heidel are taken as special cases.

Mathematical Subject Classification 2000

Primary: 34C15

Milestones

Received: 25 November 1975

Published: 1 December 1976