|
|||||

|

|
|

|

|
|
An upper bound for the
period of the simple continued fraction for 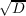
Ralph Gordon Stanton, C. Sudler and Hugh C. Williams |
|
Vol. 67 (1976), No. 2, 525–536
|
Abstract |
|
Let p(D) denote the length
of the period of the simple continued-fraction expansion of 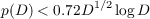 for all squarefree D > 7, and an estimate for p(D) is given when D is not squarefree. |
Mathematical Subject Classification
Primary: 10A30, 10A30
|
Milestones
Received: 10 June 1975
Revised: 19 July 1976
Published: 1 December 1976
|
Authors |
| Ralph Gordon Stanton | |
| C. Sudler | |
| Hugh C. Williams | |
| Department of Mathematics &
Statistics University of Calgary 2500 University Drive NW Calgary AB T2N 1N4 Canada |
|
 |
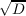 where
where 