|
|||||

|

|
|

|

|
|
Composition properties
of projective homotopy classes
Samuel S. Feder, Samuel Carlos Gitler and K. Y. Lam |
|
Vol. 68 (1977), No. 1, 47–61
|
Abstract |
|
1. Introduction. A homotopy class x ∈ πq(X) is said to be projective on X, or projectively carried by X, if it can be represented by a map that factors through the projective space pq, as shown in diagram (I), where π is the double covering map. 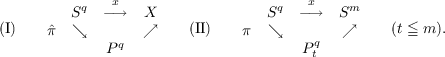
When x is a stable homotopy class of spheres, it is of interest to ask for the values of m such that x be projective on Sm. Since Sm is (t − 1)-connected for t ≦ m, this amounts to the factorisation problem posed in diagram (II) above, where π is π followed by the collapsing map from Pq to the truncated projective space Ptq = Pq∕Pt−1. We give an answer to this problem when x is a generator of the image of the J-homomorphism. |
Mathematical Subject Classification
Primary: 55E45, 55E45
|
Milestones
Received: 1 October 1975
Published: 1 January 1977
|
Authors |
| Samuel S. Feder | |
| Samuel Carlos Gitler | |
| K. Y. Lam | |
 |
