|
Let n be a positive integer, let p
be a positive continuous function on [0,∞), and consider the 2n-th order linear
differential equation
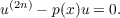 | (1) |
It is well known that this equation has a solution w = w(x) satisfying
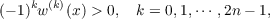 | (2) |
on [0,∞), and it is clear that w is positive and bounded. The purpose of this paper is
to investigate the essential uniqueness of the solution w, where the statement “w is
essentially unique” means that if y is any other solution of (1) which satisfies (2),
then y = kw for some nonzero constant k.
|