Measures with continuous image law

Sun Man Chang

Vol. 69 (1977), No. 1, 25–36

DOI: 10.2140/pjm.1977.69.25

Abstract

Let M be a topological space, and X a metric space. Let P(X) denote the collection of probability measures on X. Let C(M,X) denote the set of continuous functions from M to X. Let P(X) have the weak topology, and let C(M,X) have the topology of uniform convergence. For a fixed measure μ ∈ P(C(M,X)), and a member t ∈ M, define a measure tμ on X by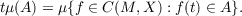

In this paper, we consider the following problem: given a continuous function T : M → P(X), when is there a measure μ ∈ P(C(M,X)) such that T(t) = tμ for all t?

Mathematical Subject Classification 2000

Primary: 28A32, 28A32

Secondary: 46E30

Milestones

Received: 22 January 1976

Revised: 13 October 1976

Published: 1 March 1977