Equations of mean curvature type in 2 independent variables

Leon M. Simon

Vol. 69 (1977), No. 1, 245–268

DOI: 10.2140/pjm.1977.69.245

Abstract

The object of this paper is to develop a regularity theory for equations of mean curvature type in two independent variables. An equation of mean curvature type in two independent variables is defined to be an equation of the form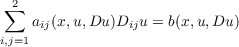

on a domain Ω ⊂ R², where the functions a_ij, b satisfy special structural conditions. Namely, we require that (i) (1 + |Du|²)^−1∕2b(x,u,Du) is bounded by a fixed constant (independent of u), and (ii) the quadratic form ∑ _i,j=1²a_ij(x,u,Du)ξ_iξ_j is bounded from above and below in terms of the quadratic form ∑ _i,j=1²g^ij(Du)ξ_iξ_j, where g^ij(Du) = δ_ij −D_iuD_ju∕(1 + |Du|²), i,j = 1,2, are the coefficients of the minimal surface equation.

Mathematical Subject Classification 2000

Primary: 49F10, 49F10

Secondary: 35J20

Milestones

Received: 16 August 1976

Published: 1 March 1977