Inner-outer factorization of functions whose Fourier series vanish off a semigroup

Howard Lewis Penn

Vol. 69 (1977), No. 2, 501–504

DOI: 10.2140/pjm.1977.69.501

Abstract

Let G be a compact, connected, Abelian group. Its dual, Γ, is discrete and can be ordered. Let Γ₁ be a semigroup which is a subset of the positive elements for some ordering, but which contains the origin of Γ. Let H^p(Γ₁) be the subspace of L^p(G) consisting of functions which have vanishing off Γ₁. The question that this paper is concerned with is what conditions on a function in H^p(Γ₁) assure an inner-outer factorization.

An inner function is a function f ∈ H^∞(Γ₁) such that |f| = 1 a.e. (dx) on G. A function f ∈ H^p(Γ₁) is said to be outer if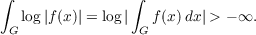

A function f ∈ H¹(Γ₁) is said to be in the class LRP(Γ₁) if log |f|∈ Γ₁(G) and log |f| has Fourier coefficients equal to zero off Γ₁ ∪−Γ₁. The main result of the paper is that if Γ₁ is the intersection of half planes and f ∈ H¹(Γ₁) with ∫ _Glog |f(x)|dx > −∞ then f has an inner-outer factorization if and only if log |f| is in LRP(Γ₁).

Mathematical Subject Classification 2000

Primary: 43A70

Secondary: 46J10

Milestones

Received: 19 November 1974

Revised: 8 November 1976

Published: 1 April 1977