Asymptotic properties of nonoscillatory solutions of differential equations with deviating argument

Ch. G. Philos and V. A. Staïkos

Vol. 70 (1977), No. 1, 221–242

DOI: 10.2140/pjm.1977.70.221

Abstract

Recently, there is an increasing interest in studying the n-th order differential equations involving the so called n-th order r-derivative of x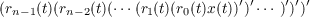

which causes damped terms. Here, the asymptotic behavior of nonoscillatory solutions of such general differential equations with deviating argument is studied and, more precisely, sufficient conditions which guarantee that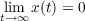

for the bounded nonoscillatory solutions x(t) are established. A basic theorem is obtained for the general case and then it is specialized into four corollaries concerning the particular case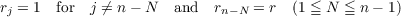

which is of special interest. Finally, some examples are given to illustrate the significance of the results.

Mathematical Subject Classification 2000

Primary: 34K20

Milestones

Received: 16 March 1976

Revised: 19 January 1977

Published: 1 May 1977