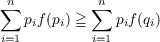|
Let
An = {P ∈ Rn : P = (p1,p2,⋯,pn), where ∑
i=1npi = 1 and pi > 0 for i = 1,2,⋯,n}
and let Bn = {P ∈ An : p1 ≧ p2 ≧⋯ ≧ pn}. We show that the inequality
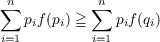 | (1) |
for all P,Q ∈ Bn and some integer n ≧ 3, implies that f(p) = clog p + d, where c is
an arbitrary nonnegative number and d is an arbitrary real number. We show,
furthermore, that if we restrict the domain of the inequality (1) to those P,Q ∈ Bn
for which P ≻ Q (Hardy-Littlewood-Pólya order), then any function that is convex
and increasing satisfies (1).
|