|

|

|
|
An unexpected surgery
construction of a lens space
James Bailey and Dale Rolfsen |
|
Vol. 71 (1977), No. 2, 295–298
|
Abstract |
|
A useful method of constructing-3-dimensional manifolds is to remove the interior of a tubular neighbourhood V ⊂ S3 of a knot K in the 3-sphere and sew it back differently, via a homeomorphism h : ∂V → ∂V . This surgery construction, due to M. Dehn, yields the manifold 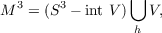 where x ∈ ∂V ⊂ V is identified with h(x) ∈ ∂V ⊂ S3 − int V . For example surgery along a trivial knot yields, for various choices of h, exactly the class of lens spaces L(p,q), including the extreme cases L(1,0)≅S3 and L(0,1)≅S2 × S1. |
Mathematical Subject Classification
Primary: 57A10, 57A10
Secondary: 55A25
|
Milestones
Received: 9 April 1975
Revised: 4 May 1976
Published: 1 August 1977
|
Authors |
| James Bailey | |
| Dale Rolfsen | |
| Mathematics Department University of British Columbia 1984 Mathematics Road Vancouver BC V6T 1Z2 Canada |
|
| http://www.math.ubc.ca/~rolfsen/ | |
 |
