|
Let X be a Hilbert space, E a
linear operator with finite dimensional null space, and N a nonlinear operator. In this
paper we study the nonlinear equation
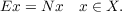 | (1) |
Equations of this form arise in the study of boundary value problems for elliptic
differential equations.
We use the alternative scheme of Bancroft, Hale, and Sweet and results from
monotone operator theory with suitable monotonicity assumptions on E and N to
reduce equation (1) to an alternative problem. We then use results from monotone
operator theory to solve the alternative problem, hence prove the existence of
solutions to equation (1). This extends to nonselfadjoint operators the results of
Cesari and Kannan.
|