|
Let p and q be indices in the
open interval (1,∞) such that pq < p + q; let r = pq∕(p + q − pq). It is shown here
that there is a constant Cp,q < 1 such that, if G is a locally compact, unimodular
group with no compact open subgroups, and if g and f are functions in Lp(G) and
Lq(G) respectively, then
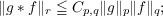
here g ∗f denotes the convolution of g and f. Thus, in this case, Young’s inequality
for convolution is not sharp; this result is used to prove a similar statement about
sharpness in Kunze’s extension of the Hausdorff-Young inequality. The best constants
in these inequalities are known in many special cases; the methods used here do
not yield good estimates for these constants, but they do lead to the first
proof of nonsharpness for general unimodular groups without compact open
subgroups.
|