W_δ(T) is convex

J. Kyle

Vol. 72 (1977), No. 2, 483–485

DOI: 10.2140/pjm.1977.72.483

Abstract

Stampfli introduced a generalization of the numerical range for any bounded linear operator T on a Hilbert space ℋ. This is denoted by W_δ(T) and is defined by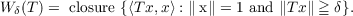

Stampfli asked whether W_δ(T) is convex. In this short note we provide an affirmative answer to this question.

Mathematical Subject Classification 2000

Primary: 47A10

Milestones

Received: 15 February 1977

Published: 1 October 1977